Java Code House

Today I am going to post a program that will be able to produce all the mColorings of a given graph G.
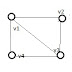
What is mColoring : The problem statement says that for a given graph G(V,E) and m colors, we have to color all the vertices the graph G with m-colors in all possible ways. This is called m-coloring of a graph G. Suppose for a graph G and 3 colors , we have to show all its 3-colorings.
How to solve the problem : Here we first define a function mColoring(int k) that will use the concept of backtracking. Here in this function we call another function next_color(int k) that will try to color the kth vertex. Now if we are successful then check whether all vertex have been colored. If it is true then we print the solution and then try another solution vector otherwise color the remaining vertex. If we were unsuccessful then we go back (backtrack)) to the last successful situation and try a different path. Our final solution i.e. all the possible m-colorings can be represented as a tree.

Graph G to be colored

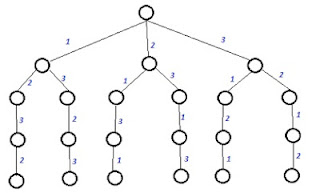Tree for 3-coloring of graph G

--------------------------------------------------------------------------------------------------------------------------

public class MWayGrColor{
    /*G is graph's adjacency matrix and x is solution vector */
    private int G[][],x[],n,m,soln;

    public void mColoring(int k){  //backtracking function
        for(int i=1;i<=n;i++){
           next_color(k);  //coloring kth vertex
           if(x[k]==0)
              return;  //if unsuccessful then backtrack
           if(k==n)  //if all colored then show
              write();
           else
              mColoring(k+1);  /* successful but still left to color */
        }
   }

   private void next_color(int k){
      do{
           int i=1;
         x[k]=(x[k]+1)%(m+1);
         if(x[k]==0)
           return;
         for(i=1;i<=n;i++)
            if(G[i][k]!=0 && x[k]==x[i])  /* checking adjacency and not same color */
               break;
         if(i==n+1)   return;  //new color found
      }while(true);
   }

   private void write(){
      System.out.print("\nColoring(V C) #  "+(++soln)+"-->");
      for(int i=1;i<=n;i++)
          System.out.print("\t("+i+" "+x[i]+")");  //solution vector
   }
   
   public void input(){
         java.util.Scanner sc=new java.util.Scanner(System.in);
         System.out.print("Enter no. of vertices : ");
         n=sc.nextInt();
         G=new int[n+1][n+1];
         x=new int[n+1];
         System.out.print("Enter no. of colors : ");
         m=sc.nextInt();
        System.out.println("Enter adjacency matrix-->");
        for(int i=1;i<=n;i++)
           for(int j=1;j<=n;j++)
               G[i][j]=sc.nextInt();
   }
   
   public static void main (String[] args) {
        MWayGrColor obj=new MWayGrColor();
        obj.input();
        obj.mColoring(1);
        if(obj.soln==0)
           System.out.println("\nNeed more than "+obj.m+" colors");
        else
           System.out.print("\nTOTAL SOLN : "+obj.soln);
   }
}