Java Code House

Today in this article I will show you how to solve 0-1 Knapsack problem using the concept of dynamic programming in Java. This problem can also be solved by recursion but the problem is that it will result in solving of already solved sub-problem. So we will be using dynamic programming to solve by storing the results of solved sub-problems. Also this technique can be used to solve the problem in polynomial time. The complexity of solving it using this algorithm is O(n*W).
What is 0/1 Knapsack problem ?
The knapsack or rucksack problem is a problem in combinatorial optimization. Here there are a set of items(n) which has a profit value(v) and weight(w). There is a bag which has a maximum capacity(W). Now the problem is to fill the bag with the following restrictions :
   1. You can either choose an item completely or reject it. (0 or 1)
   2. The total weight of bag must not exceed its maximum capacity W. i.e. (Sum of w[i]) <= W
   3.  The total value or profit of items chosen must be maximum. i.e. Sum of p[i] is maximum
where 0 <  i <=n.
How to solve 0/1 Knapsack problem in Java ?
Step1: Structure: Characterize the structure of an optimal solution.
    – Decompose the problem into smaller problems, and find a relation between the structure of the optimal solution of the original problem and the solutions of the smaller problems.

Today I am going to show how to convert a postfix expression to an infix expression using stack in Java. In an earlier post here we ahve shown how to convert an infix expression to postfix using stack. Here we will just try to do the reverse. Here in our example we will be able to convert any postfix expression to infix irrespective of the operators. A number of parenthesis may be generated extra which were not there in original infix expression. The parenthesis that may be generated extra will have no impact on actual expression, they are just for better understanding. The process of postfix to infix conversion is summarised below -

Today in this article I will tell you how to convert an infix expression to postfix expression using stack. This is an important application of stack. Most of the codes that you will find dont take into considerations the exponent and parenthesis. Here in our example we will consider everything and it will be able to convert any infix expression to postfix containing exponent(^) and parenthesis("(",")"). In our example we have also shown the current symbol processed, stack status and current postfix expression. We have solved it in the following way

• First push a sentinel element # to denote end of stack
• Scan each symbol of input infix expression
• If symbol is operator then check precedence with operator on stack top and take necessary action
• If left parenthesis then push it, and if right parenthesis then pop continously from stack till a left parenthesis is found
• If all symbols are scanned then pop all elements from stack and ad to postfix till # found.

import java.util.Scanner;
import java.util.Stack;

public class InfixToPostfix {

 /**
  * Checks if the input is operator or not
  * @param c input to be checked
  * @return true if operator
  */
 private boolean isOperator(char c){
  if(c == '+' || c == '-' || c == '*' || c =='/' || c == '^')
   return true;
  return false;
 }
 
 /**
  * Checks if c2 has same or higher precedence than c1
  * @param c1 first operator
  * @param c2 second operator
  * @return true if c2 has same or higher precedence
  */
 private boolean checkPrecedence(char c1, char c2){
  if((c2 == '+' || c2 == '-') && (c1 == '+' || c1 == '-'))
   return true;
  else if((c2 == '*' || c2 == '/') && (c1 == '+' || c1 == '-' || c1 == '*' || c1 == '/'))
   return true;
  else if((c2 == '^') && (c1 == '+' || c1 == '-' || c1 == '*' || c1 == '/'))
   return true;
  else
   return false;
 }
 
 /**
  * Converts infix expression to postfix
  * @param infix infix expression to be converted
  * @return postfix expression
  */
 public String convert(String infix){
  System.out.printf("%-8s%-10s%-15s\n", "Input","Stack","Postfix");
  String postfix = "";  //equivalent postfix is empty initially
  Stack<Character> s = new Stack<>();  //stack to hold symbols
  s.push('#');  //symbol to denote end of stack

  System.out.printf("%-8s%-10s%-15s\n", "",format(s.toString()),postfix);  

  for(int i = 0; i < infix.length(); i++){
   char inputSymbol = infix.charAt(i);  //symbol to be processed
   if(isOperator(inputSymbol)){  //if a operator
    //repeatedly pops if stack top has same or higher precedence
    while(checkPrecedence(inputSymbol, s.peek()))
     postfix += s.pop();
    s.push(inputSymbol);
   }
   else if(inputSymbol == '(')
    s.push(inputSymbol);  //push if left parenthesis
   else if(inputSymbol == ')'){
    //repeatedly pops if right parenthesis until left parenthesis is found
    while(s.peek() != '(') 
     postfix += s.pop();
    s.pop();
   }
   else
    postfix += inputSymbol;
   System.out.printf("%-8s%-10s%-15s\n", ""+inputSymbol,format(s.toString()),postfix);  
  }

  //pops all elements of stack left
  while(s.peek() != '#'){
   postfix += s.pop();
   System.out.printf("%-8s%-10s%-15s\n", "",format(s.toString()),postfix);  

  }
  
  return postfix;
 }
 
 /**
  * Formats the input  stack string
  * @param s It is a stack converted to string
  * @return formatted input
  */
 private String format(String s){
  s = s.replaceAll(",","");  //removes all , in stack string
  s = s.replaceAll(" ","");  //removes all spaces in stack string
  s = s.substring(1, s.length()-1);  //removes [] from stack string
  
  return s;
 }
 
 public static void main(String[] args) {
  InfixToPostfix obj = new InfixToPostfix();
  Scanner sc = new Scanner(System.in);
  System.out.print("Infix : \t");
  String infix = sc.next();
  System.out.print("Postfix : \t"+obj.convert(infix));
 }
}

-------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------

Infix :         A+(B*C-(D/E^F)*G)*H
Input   Stack     Postfix
        #
A       #         A
+       #+        A
(       #+(       A
B       #+(       AB
*       #+(*      AB
C       #+(*      ABC
-       #+(-      ABC*
(       #+(-(     ABC*
D       #+(-(     ABC*D
/       #+(-(/    ABC*D
E       #+(-(/    ABC*DE
^       #+(-(/^   ABC*DE
F       #+(-(/^   ABC*DEF
)       #+(-      ABC*DEF^/
*       #+(-*     ABC*DEF^/
G       #+(-*     ABC*DEF^/G
)       #+        ABC*DEF^/G*-
*       #+*       ABC*DEF^/G*-
H       #+*       ABC*DEF^/G*-H
        #+        ABC*DEF^/G*-H*
        #         ABC*DEF^/G*-H*+
Postfix :       ABC*DEF^/G*-H*+

-------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------
DOWNLOAD the source from Mediafire
DOWNLOAD the source from 4shared

Today I will show you how you can implement Bankers algorithm in Java. The Banker's algorithm is a resource allocation and deadlock avoidance algorithm that tests for safety by simulating the allocation of predetermined maximum possible amount of all resources, and then makes a check to test for possible deadlock conditions for all other pending activities, before deciding whether allocation should be allowed to continue. Here we have 3 input matrix where
max[][] - denotes maximum resources that will be required by processes
allocate[][] - denotes currently allocated resources to processes
avail[][] - denotes resources available in the system
We will calculate need matrix and then try to allocate. I f we can allocate safely then give a suitable message.

--------------------------------------------------------------------------------------------------------------------------

Today I am going to show how you can create your own stack using linked list. Hope that you already know how to create a stack. But that stack can take input of only one type of objects. For different types you have to write seperate programs. But this can be avoided if we use java.lang.Object as data type for stack elements. But if you use this then a problem will arise. When you are pushing into stack then you can push any object in this case. But while popping you won't be able to understand the data type of the elements and so won't be able to typecast and use it properly and hence not type safe. So a new feature GENERICS was introduced to make it type safe. Using generics you can only insert one type of object , only you have to mention about data type during creating stack object and thus only need to create seperate stack objects and not programs. The following code will explain better.
--------------------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------------------
/* The STACK class */

public class Stack<T> {
    //T is the type parameter
    Node top; //topmost element of stack

    //defines each node of stack
    class Node{
       T value; //value of each node
       Node next;  //pointer to next node
 
       public Node(T value){
         this.value=value;  //initializing
         next=null;
       }
    }
    //This function pushes new element
    public void push(T value){
     Node current=new Node(value);
     if(isEmpty())
        top=current; //if empty stack
     else{
        current.next=top;
        top=current;
     }
    }
    //This function pops topmost element
    public T pop(){
     T value=null;
     if(!isEmpty()){
         top=top.next;
         value=top.value;
     }
     return value;  //returning popped value
    }
    //This function returns the entire stack
    public String toString(){
     Node current=top;
        StringBuilder s=new StringBuilder();
     System.out.println("\n---------------STACK--------------");
     
     while(current!=null){
       s.append(current.value+"  ");
       current=current.next;
     }

        return s.toString();
    }
    //This function returns topmost element
    public T peek(){
     return top.value;
    }
    //This function checks emptiness of stack
    public boolean isEmpty(){
     return (top==null)?true:false;
    }    
}

/* The main class testing stack */

public class Test{
    public static void main(String[] args) {
        //creating and using stack of integers
        Stack<Integer> s=new Stack<Integer>();
        s.push(15);  s.push(10);  s.push(12);
        System.out.println(s);
        s.pop();  s.pop();
        System.out.println(s);

        //creating and using stack of floats
        Stack<Float> s2=new Stack<Float>();
        s2.push(5.5f);  s2.push(1.2f);  s2.push(8.6f);
        System.out.println(s2);
        s2.pop();  s2.pop();
        System.out.println(s2);
    }
}

--------------------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------------------

---------------STACK--------------
12  10  15

---------------STACK--------------
15

---------------STACK--------------
8.6  1.2  5.5

---------------STACK--------------
5.5

--------------------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------------------

Today I am going to post a program that will be able to produce all the mColorings of a given graph G.
What is mColoring : The problem statement says that for a given graph G(V,E) and m colors, we have to color all the vertices the graph G with m-colors in all possible ways. This is called m-coloring of a graph G. Suppose for a graph G and 3 colors , we have to show all its 3-colorings.
How to solve the problem : Here we first define a function mColoring(int k) that will use the concept of backtracking. Here in this function we call another function next_color(int k) that will try to color the kth vertex. Now if we are successful then check whether all vertex have been colored. If it is true then we print the solution and then try another solution vector otherwise color the remaining vertex. If we were unsuccessful then we go back (backtrack)) to the last successful situation and try a different path. Our final solution i.e. all the possible m-colorings can be represented as a tree.

Graph G to be colored

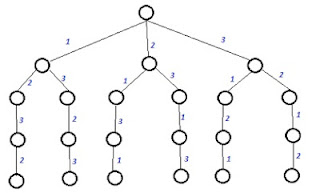Tree for 3-coloring of graph G

--------------------------------------------------------------------------------------------------------------------------

public class MWayGrColor{
    /*G is graph's adjacency matrix and x is solution vector */
    private int G[][],x[],n,m,soln;

    public void mColoring(int k){  //backtracking function
        for(int i=1;i<=n;i++){
           next_color(k);  //coloring kth vertex
           if(x[k]==0)
              return;  //if unsuccessful then backtrack
           if(k==n)  //if all colored then show
              write();
           else
              mColoring(k+1);  /* successful but still left to color */
        }
   }

   private void next_color(int k){
      do{
           int i=1;
         x[k]=(x[k]+1)%(m+1);
         if(x[k]==0)
           return;
         for(i=1;i<=n;i++)
            if(G[i][k]!=0 && x[k]==x[i])  /* checking adjacency and not same color */
               break;
         if(i==n+1)   return;  //new color found
      }while(true);
   }

   private void write(){
      System.out.print("\nColoring(V C) #  "+(++soln)+"-->");
      for(int i=1;i<=n;i++)
          System.out.print("\t("+i+" "+x[i]+")");  //solution vector
   }
   
   public void input(){
         java.util.Scanner sc=new java.util.Scanner(System.in);
         System.out.print("Enter no. of vertices : ");
         n=sc.nextInt();
         G=new int[n+1][n+1];
         x=new int[n+1];
         System.out.print("Enter no. of colors : ");
         m=sc.nextInt();
        System.out.println("Enter adjacency matrix-->");
        for(int i=1;i<=n;i++)
           for(int j=1;j<=n;j++)
               G[i][j]=sc.nextInt();
   }
   
   public static void main (String[] args) {
        MWayGrColor obj=new MWayGrColor();
        obj.input();
        obj.mColoring(1);
        if(obj.soln==0)
           System.out.println("\nNeed more than "+obj.m+" colors");
        else
           System.out.print("\nTOTAL SOLN : "+obj.soln);
   }
}